Answer:
a)
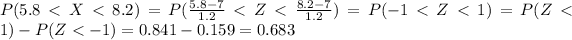
b)

c) For part a we are just finding the probability that an individual baby would have a weight between 5.8 and 8.2. So we can't compare the result of part a with the result for part b.
For part b we are finding the probability that the mean of 9 babies (from random sampling) would be between 5.8 and 8.2, so on this case we have a distribution with a different deviation depending on the sample size. And for this reason we have different values
Explanation:
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean". The letter
 is used to denote the cumulative area for a b quantile on the normal standard distribution, or in other words:
is used to denote the cumulative area for a b quantile on the normal standard distribution, or in other words:

Let X the random variable that represent the weights of full-term newborn babies of a population, and for this case we know the distribution for X is given by:
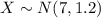
a. What is the probability that one newborn baby will have a weight within 1.2 pounds of the meanlong dashthat is, between 5.8 and 8.2 pounds, or within one standard deviation of the mean?
We are interested on this probability
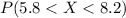
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
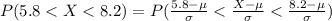
And in order to find these probabilities we can find tables for the normal standard distribution, excel or a calculator.
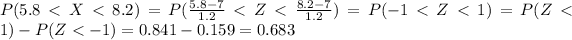
b. What is the probability that the average of nine babies' weights will be within 1.2 pounds of the mean; will be between 5.8 and 8.2 pounds?
And let
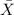 represent the sample mean, the distribution for the sample mean is given by:
represent the sample mean, the distribution for the sample mean is given by:

On this case
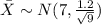
The z score on this case is given by this formula:
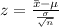
And if we replace the values that we have we got:

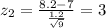
For this case we can use a table or excel to find the probability required:

c. Explain the difference between (a) and (b).
For part a we are just finding the probability that an individual baby would have a weight between 5.8 and 8.2. So we can't compare the result of part a with the result for part b.
For part b we are finding the probability that the mean of 9 babies (from random sampling) would be between 5.8 and 8.2, so on this case we have a distribution with a different deviation depending on the sample size. And for this reason we have different values