Question

In the kite , AK=9 , JK=15 , and AM=16 .

What is JM ?

Enter your answer in the box.

Kite J K L M with shorter diagonal J L intersecting longer diagonal K M at point A.

Answer 1

The Length of JM is 20.

Explanation:

Given,

JKLM is a kite in which JL and KM are the diagonals that intersect at point A.

Length of AK = 9

Length of JK = 15

Length of AM = 16

Solution,

Since JKLM is a kite. And JL and KM are the diagonals.

And we know that the diagonals of a kite perpendicularly bisects each other.

So, JL ⊥ KM.

Therefore ΔJAK is aright angled triangle.

Now according to Pythagoras Theorem which states that;

"The square of the hypotenuse is equal to the sum of the square of base and square of perpendicular".

`JK^2=KA^2+AJ^2`

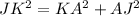
On putting the values, we get;

`(15)^2=9^2+AJ^2\\\\225=81+AJ^2\\\\AJ^2=225-81=144`

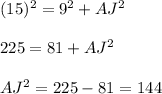
On taking square root onboth side, we get;

`√(AJ^2) =√(144)\\\\AJ=12`

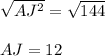
Again By Pythagoras Theorem,

`AJ^2+AM^2=JM^2`

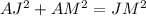
On putting the values, we get;

`JM^2=(12)^2+(16)^2\\\\JM^2=144+256=400`

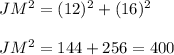
On taking square root onboth side, we get;

`\sqrt {JM^2}=√(400)\\\\JM=20`

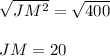
Hence The Length of JM is 20.