Question

Simplify: (sin θ − cos θ)2 − (sin θ + cos θ)2

a. -4sin(θ)cos(θ)
b. 2
c. sin^2θ
d. cos^2θ

Answer 1

The Solution is below. That is the option a. -4sin (θ)cos (θ)

Explanation:

Simplify: (sin θ − cos θ)2 − (sin θ + cos θ)2

Solution:

We know the Identity

`A^(2)- B^(2)=(A+B)(A-B)`

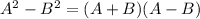
Applying this Identity we get

`(\sin \theta - \cos \theta)^(2) -(\sin \theta + \cos \theta)^(2) =((\sin \theta - \cos \theta)+(\sin \theta + \cos \theta))((\sin \theta - \cos \theta)-(\sin \theta + \cos \theta))\\`

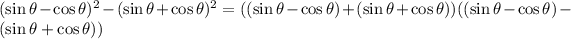
Now Plus sin θ Minus sin θ and Plus cos θ Minus cos θ will cancel each other then we have,

`(\sin \theta - \cos \theta)^(2) -(\sin \theta + \cos \theta)^(2) =(2\sin \theta)(-2\cos \theta)\\(\sin \theta - \cos \theta)^(2) -(\sin \theta + \cos \theta)^(2) =-4\sin \theta\cos \theta\\\\As\ Required\ in\ option\ a.`

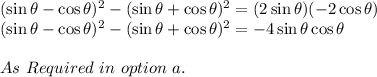
The Solution is the option a. -4sin (θ)cos (θ)