Question

Assume that a sample is used to estimate a population proportion p. Find the margin of error E that corresponds to the given statistics and confidence level. Round the margin of error to four decimal places. In a clinical test with 2400 subjects, 720 showed improvement from the treatment. Find the margin of error for the 99% confidence interval used to estimate the population proportion.

Answer 1

Answer: 0.0241

Explanation:

The formula we use to find the margin of error :

`E=z^*\sqrt{(p(1-p))/(n)}`

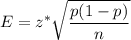
, where z* = Critical value , n= Sample size and p = Sample proportion.

As per given , we have

n= 2400

Sample proportion of subjects showed improvement from the treatment:

`p=(720)/(2400)=0.3`

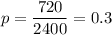
Critical value for 99% confidence = z*= 2.576 (By z-table)

Now , the margin of error for the 99% confidence interval used to estimate the population proportion. :

`E=(2.576)\sqrt{(0.3(1-0.3))/(2400)}`

`E=(2.576)√(0.0000875)`

`E=(2.576)(0.00935414346693)`

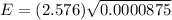
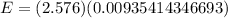
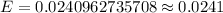`E=0.0240962735708\approx0.0241` [Round to the four decimal places]

Hence, the margin of error for the 99% confidence interval used to estimate the population proportion. =0.0241