Question

A landscaper puts 5 fish into a new pond. The number of fish doubles each month over a period of time.

Write a function f(x) to model the number of fish in the pond after x months,

Answer 1

F(x) = 5 (2)^x-1

Explanation:

If the number of fish doubles each month over a period of time, the sequence may thus be expressed as

5, 10, 20, 40....

This is a geometric sequence with 5 as the first term and 2 as the common ratio.

The function f(x) to model the number of fish in the pond after x months may then be expressed as the nth term

F(x) = 5 (2)^x-1

Answer 2

The function f(x) to model the number of fish in the pond after x months is given as function f(x) =
`5(2)^x`

Solution:

Given that landscaper puts 5 fish into a new pond

The number of fish doubles each month over a period of time

To find: function f(x) to model the number of fish in the pond after x months

From given information,

Number of fish doubles each month and initially there put 5 fish into pond

Number of fish after 1 month = 5(2)

Number of fish after 2 months = 5(2)(2) =
`5^2`

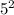
Number of fish after 3 months = 5(2)(2)(2) =
`5^3`

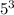
Number of fish after 4 months = 5(2)(2)(2)(2)
`5^4`

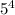
So after "x" months, number of fish in pond is given as,

number of fish in pond =
`5(2)^x`

function f(x) =
`5(2)^x`

Thus the required function is found