Question

Suppose that the proportion of young adults who read at least one book per month is 0.15, and this proportion is the same in Boston and New York. Suppose that samples of size 400 are randomly drawn from each city. The standard deviation for the sampling distribution of differences between the first sample proportion and the second sample proportion (used to calculate the z score) is _______.

Answer 1

Answer: 0.025

Explanation:

The standard deviation for the sampling distribution of differences between the first sample proportion and the second sample proportion is given by :_

`\sigma_(p_1-p_2)=\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)}`

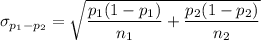
, where
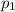`p_1`= First population proportion.

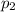`p_2`= Second population proportion

`n_1` = First sample size

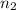`n_2` = Second sample size

As per given , we have

`p_1=0.15`

`p_2=0.15`

`n_1=400`

`n_2=400`

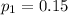
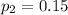
Then ,
`\sigma_(p_1-p_2)=\sqrt{(0.15(1-0.15))/(400)+(0.15(1-0.15))/(400)}`

`\sigma_(p_1-p_2)=√(0.00031875+0.00031875)`

`\sigma_(p_1-p_2)=√(0.0006375)`

`\sigma_(p_1-p_2)=0.0252487623459\approx0.025`

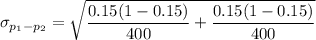
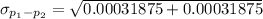
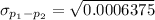
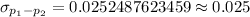
Hence, the standard deviation for the sampling distribution of differences between the first sample proportion and the second sample proportion (used to calculate the z score) is 0.025 .