Question

Solve the following systems of inequalities and select the correct graph:

2x − y > 4
x + y < −1

In each graph, the area for f(x) is shaded and labeled A, the area for g(x) is shaded and labeled B, and the area where they have shading in common is labeled AB.

If someone could show me a created graph for this, that would be great!

Answer 1

The graph in the attached figure

Explanation:

we have

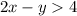`2x-y>4` ----> inequality A

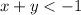`x+y<-1` ----> inequality B

The solution for the inequality A is the shaded area below the dashed line
`2x-y=4`

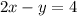
The slope of the dashed line f(x) is positive m=2

The y-intercept of the dashed line f(x) is (0,-4)

The x-intercept of the dashed line f(x) is (2,0)

The solution for the inequality B is the shaded area below the dashed line
`x+y=-1`

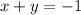
The slope of the dashed line g(x) is negative m=-1

The y-intercept of the dashed line g(x) is (0,-1)

The x-intercept of the dashed line g(x) is (-1,0)

using a graphing tool

see the area where they have shading in common

The graph in the attached figure