Question

The inequality x + 12x + 35 has two critical points and three possible intervals for solutions. Choose

each set of possible test points for the three intervals.


-8,-6,4


-10, -6,0


-6,0,6


-6,0, 10

Answer 1

Option 1 and 2.

Explanation:

Consider he given inequality is

`x^2 + 12 x+35\ge0`

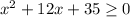
Splitting the middle term we get

`x^2 +7x+5x+35\ge0`

`x(x+7)+5(x+7)\ge0`

`(x+5)(x+7)\ge0`

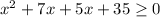
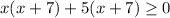
The related equation is

`(x+5)(x+7)=0`

Using zero product property we get

`x+5=0\Rightarrow x=-5`

`x+7=0\Rightarrow x=-7`

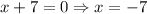
Draw number line and mark -5 and -7 on it.

Now the three intervals are (-∞ , -7], [-7,-5] and [-5,∞).

The set of possible test points for

⇒ (-∞ , -7] → -8, -10

⇒ [-7,-5] → -6

⇒ [-5,∞) → -4, 0, 4, 6

-8,-6,-4 and -10,-6,0 satisfies the given condition.

Therefore, the correct options are 1 and 2.