Question

Two sides of a triangle have the following measures: 15 and 39. What is the range of possible measures for the third side?

A) 15 < x < 24
B) 24 < x < 39
C) 24 < x < 54
D) 39 < x < 54

Answer 1

Option C) 24 < x < 54

Explanation:

we know that

The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side

Let

x ----> the measure of the third side

Applying the triangle inequality theorem

1)
`15+39 > x`

`54 > x`

Rewrite

`x < 54\ units`

2)
`x+15> 39`

`x > 39-15`

`x > 24\ units`

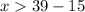
therefore

The range of possible measures for the third side is the interval (24,54)