Answer:
what type of test is this?
2. This is a right-tailed test
(b) What is the test statistic?
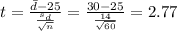
(c) Use software to get the P-value of the test statistic. Round to 4 decimal places.P-value = _____
First we need to calculate the degrees of freedom given by:
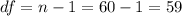
Now we can calculate the p value, since we have a right tailed test the p value is given by:

And we can use the following excel code: "=1-T.DIST(2.77,59,TRUE)"
(d) What is the conclusion regarding the null hypothesis?1. reject H02. fail to reject H0
1. reject H0
e) Choose the appropriate concluding statement.
1. The data supports the claim that retaking the SAT increases the score on average by more than 25 points.
Explanation:
Data given
 represent the sample mean difference
represent the sample mean difference
 represent the sample standard deviation
represent the sample standard deviation
n=60 represent the sample size selected
 represent the significance level
represent the significance level
Confidence =1-0.05=0.95
System of Hypothesis
The system of hypothesis for this case are:
Null hypothesis:
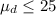
Alternative hypothesis:
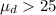
what type of test is this?
2. This is a right-tailed test
(b) What is the test statistic?
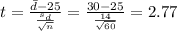
(c) Use software to get the P-value of the test statistic. Round to 4 decimal places.P-value = _____
First we need to calculate the degrees of freedom given by:
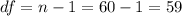
Now we can calculate the p value, since we have a right tailed test the p value is given by:

And we can use the following excel code: "=1-T.DIST(2.77,59,TRUE)"
(d) What is the conclusion regarding the null hypothesis?1. reject H02. fail to reject H0
1. reject H0
e) Choose the appropriate concluding statement.
1. The data supports the claim that retaking the SAT increases the score on average by more than 25 points.