Question

Given the following system of equations:

−4x + 8y = 16
2x + 4y = 8

What action was completed to create this new equivalent system of equations?

−2x + 4y = 8
2x + 4y = 8

(A) Multiply the second equation, 2x + 4y = 8, by −1.
(B) Multiply the first equation, −4x + 8y = 16, by −1.
(C) Divide the second equation, 2x + 4y = 8, by 2.
(D) Divide the first equation, −4x + 8y = 16, by 2.v

Answer 1

d, or divide the first equation.

Explanation:

Answer 2

(D) Divide the first equation,
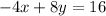`-4x + 8y = 16` , by 2.

Explanation:

Given:

`-4x + 8y = 16 \ \ \ \ equation \ 1`

`2x + 4y = 8 \ \ \ \ equation \ 2`

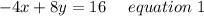
We need to find the operation performed on equation so as to get resultant equation as:

`-2x + 4y = 8`

`2x + 4y = 8`

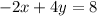
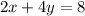
From Above we can see that there is no change in equation 2 with respect to resultant equation.

Also Resultant equation is simplified form of equation 1.

Simplifying equation 1 we get;

`-4x + 8y = 16`

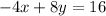
We can see that 2 is the common multiple on both side.

Hence we will divide equation 1 with 2 we get

`(-4x)/(2)+(8y)/(2)=(16)/(2)\\\\-2x+4y=8`

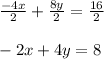
which is the resultant equation.

Hence (D) Divide the first equation,
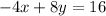`-4x + 8y = 16` , by 2 is the correct option.