Question

Triangle ABC has vertices at A(−3, 4), B(4, −2), C(8, 3). The triangle translates 2 units up and 1 unit right. Which rule represents the translation? After the translation, what are the coordinates of vertex A?

Answer 1

The translation statement is given by:

`(x,y)\rightarrow (x+1,y+2)`

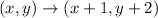
After the translation, the coordinates of vertex A is (-2,6).

Explanation:

Given :

Vertices of a triangle ABC are:

A(−3, 4), B(4, −2), C(8, 3)

The triangle is translated 2 units up and 1 unit right.

To find the co-ordinates of point A after translation.

Translation rules.

For shift of
`c` units up, the translation is given as:

`(x,y)\rightarrow (x,y+c)`

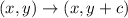
For shift of
`k` units right, the translation is given as:

`(x,y)\rightarrow (x+k,y)`

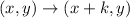
So, it says the triangles is translated 2 units up and 1 unit right.

The translation statement is given by:

`(x,y)\rightarrow (x+1,y+2)`

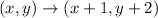
So, co-ordinates of point A after translation is given by :

`(-3,4)\rightarrow (-3+1,4+2)=(-2,6)`

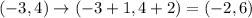
After the translation, the coordinates of vertex A is (-2,6).