Answer:
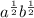
Explanation:
Given:
The expression in radical form is given as:
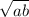
We need to express this in fractional exponent form.
We know that,
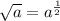
Also,
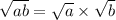
Now, clubbing both the properties of square root function, we can rewrite the given expression as:
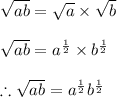
So, the given expression in fractional exponents form is
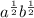 .
.