Answer:
The graph stretches horizontally by a factor of 4 and shifted up by 1 unit.
Explanation:
Given:
The function
 is given as:
is given as:
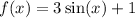
The function
 is given as:
is given as:

The function 'g' can be rewritten as:
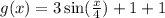
So, the 'x' value of 'f' is multiplied by
 and 1 unit is added to the function to get the function 'g'.
and 1 unit is added to the function to get the function 'g'.
Therefore, as per transformation rules:
1.
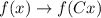
- If C > 1 ⇒ The graph compresses in the x direction.
- If 0 < C < 1 ⇒ The graph stretches in the x direction by factor of 1/C.
2.
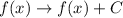
- If C > 0 ⇒ The graph shifts up by 'C' units.
- If C < 0 ⇒ The graph shifts down by 'C' units.
Therefore, the graph of
 stretches in the x direction(horizontally) by a factor of 4 and shifts up by 1 unit to get
stretches in the x direction(horizontally) by a factor of 4 and shifts up by 1 unit to get
 .
.