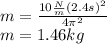Answer:
a)
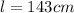
b)
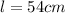
c)
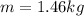
d)
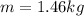
Step-by-step explanation:
The period is defined as:

Here,
 is the natural frequency of the system.
is the natural frequency of the system.
In a pendulum is given by:
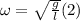
Replacing (2) in (1) and solving for l:

a) On Earth:
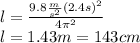
b) On Mars:
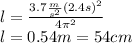
In a mass-spring system, the natural frequency is:

Replacing (3) in (1) and solving for m:
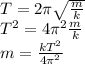
c) On Earth:
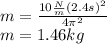
d) On Mars: