Question

Unfortunately, arsenic occurs naturally in some ground water†. A mean arsenic level of µ = 8.0 parts per billion (ppb) is considered safe for agricultural use. A well in Texas is used to water cotton crops. This well is tested on a regular basis for arsenic. A random sample of 36 tests gave a sample mean of x = 7.3 ppb arsenic, with s = 2.4 ppb. Does this information indicate that the mean level of arsenic in this well is less than 8 ppb? Use a = 0.05.(a) What is the level of significance?State the null and alternate hypotheses.H0: µ < 8 ppb; H1: µ = 8 ppb H0: µ > 8 ppb; H1: µ = 8 ppb H0: µ = 8 ppb; H1: µ ? 8 ppb H0: µ = 8 ppb; H1: µ > 8 ppb H0: µ = 8 ppb; H1: µ < 8 ppb(b) What sampling distribution will you use? Explain the rationale for your choice of sampling distribution.The standard normal, since the sample size is large and s is known. The standard normal, since the sample size is large and s is unknown. The Student's t, since the sample size is large and s is unknown. The Student's t, since the sample size is large and s is known.What is the value of the sample test statistic? (Round your answer to three decimal places.)(c) Find the P-value. (Round your answer to four decimal places.)Sketch the sampling distribution and show the area corresponding to the P-value.(d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? Are the data statistically significant at level a?At the a = 0.05 level, we reject the null hypothesis and conclude the data are not statistically significant. At the a = 0.05 level, we reject the null hypothesis and conclude the data are statistically significant. At the a = 0.05 level, we fail to reject the null hypothesis and conclude the data are statistically significant. At the a = 0.05 level, we fail to reject the null hypothesis and conclude the data are not statistically significant.(e) Interpret your conclusion in the context of the application.There is insufficient evidence at the 0.05 level to reject the claim that the mean level of arsenic in the well is not less than 8 ppb. There is sufficient evidence at the 0.05 level to reject the claim that the mean level of arsenic in the well is not less than 8 ppb.

Answer 1

Check the explanation below.

Explanation:

Hello!

The study variable is:

X: Arsenic level of well water (ppb)

If the mean concentration of arsenic is 8 ppb then the water is considered safe to use for agricultural use.

In texas a sample of 36 tests for arsenic was taken to see if the average level of arsenic of the water well is less than 8 ppb, symbolically μ < 8

The hypothesis is:

a)

H₀: μ ≥ 8

H₁: μ < 8

Level of significance is α: 0.05

b)

To study the population mean the variable needs to have at least a normal distribution. If the information of the sample was available we could make a normality test to check if it's distribution is normal or not. Since the Students t cannot be used unless the variable has a normal distribution, we cannot choose this statistic to make the hypothesis test, the same happens with the standard normal, if the condition of a variable with normal distribution is not met, the statistic cannot be used.

The most recommendable is to apply the Central Limit Theorem, this theorem states:

Be a population with probability function f(X;μ,δ²) from which a random sample of size n is selected. Then the distribution of the sample mean tends to the normal distribution with mean μ and variance δ²/n when the sample size tends to infinity.

As a rule, a sample of size greater than or equal to 30 is considered sufficient to apply the theorem and use the approximation.

X[bar]≈N(μ; σ²/n)

Then you can use the standard normal approximation:

Z= X[bar] - μ ≈N(0;1)

σ/√n

The critical region for this test is one-tailed (left tail)

`Z_(\alpha ) = Z_(0.05)= -1.645`

If
`Z_(H_0) \leq -1.645\\`, you reject the null hypothesis.

If
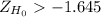`Z_(H_0) > -1.645`, you do not reject the null hypothesis.

c)

The statistic is:

`Z= (7.3-8)/((2.4)/(√(36) ) )`

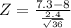
Z= -1.75

The p-value is one-tailed with the same direction of the test, you calculate it as:

P(Z < -1.75)= 0.04006

To decide using the p-value you have to compare it against the significance level.

If it is greater than the level of significance, then you don't reject the null hypothesis.

If it is equal or less than the level of significance, then you reject the null hypothesis.

d) The calculated p-value (0.04006) is less than α (0.05), the decision is to reject the null hypothesis.

e) At a level of 5%, the decision is to reject the null hypothesis. This means that there is significant evidence to think that the average level of arsenic in the well water is less than 8 ppb.

I hope it helps!