Answer:
b0= 144.59
b= -2.12
Se²= 1.02
99%CI E(Y/X=35): [68.78; 71.99]
Explanation:
Hello!
I've arranged the given data:
X: 37.0, 36.4, 35.8, 34.3, 33.7, 32.1, 31.5
Y: 65.0, 67.2, 70.3, 71.9, 73.8, 75.7, 77.9
The equation of the linear regression model is:
Yi= β₀ + βXi + εi
Where
Yi is the dependent variable
Xi is the independent variable
εi represents the errors or residues
β₀ is the intercept of the line
β is the slope
The conditions to make a linear regression analysis are:
For each given value of X, there is a population of Y~N(μy;σy²)
Each value of Y is independent of the others.
The population variances of each population of Y are equal.
From these conditions the following characteristic is deduced:
εi~N(0;σ²)
The parameters of the regression are:
β₀, β, and σ²
If the conditions are met then you can estimate the regression line:
Yi= bo * bXi + ei.
And the point estimation of the parameters can be calculated using the formulas:
β₀ ⇒ b0= (∑y/n)-b(∑x/n)
β ⇒ b= [∑xy- ((∑x)(∑y))/n]/(∑x²-((∑x)²/n))
σ²⇒ Se²= 1/(n-2)*[∑y²-(∑y)²/n - b²(∑x²-(∑x)²/n)]
n= 7
∑y= 501.80
∑y²= 36097.88
∑x= 240.80
∑x²= 8310.44
∑xy= 17204.87
b0= 144.59
b= -2.12
Se²= 1.02
The estimated regression line is:
Yi= 144.59 -2.12Xi
You need to calculate a 99%CI E(Y/X=35), the formula is:
(b0 + bX0) ±
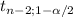 *
*
![\sqrt{S_e^2((1)/(n)+((X_0-X[bar])^2)/(sumX^2-(((sumX)^2)/(n) )) )}](https://img.qammunity.org/2020/formulas/mathematics/college/qgjeth3womn1dttbcz7sv1uajdpbd7z2eb.png)
(144.59 + (-2.12*35)) ± 4.032*

[68.78; 71.99]
With a 99% confidence level youd expect that the interval [68.78; 71.99] contains the true value of the average of Y when X= 35.
I hope it helps!