Answer:
The value of the test statistic and degrees of freedom is 2.148 and 11 respectively.
Explanation:
Consider the provided information.
The mean annual tuition and fees for a sample of 12 private colleges was 36,800 with a standard deviation of 5,000 .
Thus, n = 12,
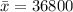 σ = 5000
σ = 5000
degrees of freedom = n-1 = 12-1 = 11
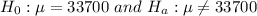
Formula to find the value of z is:
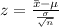
Where
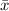 is mean of sample, μ is the mean of population, σ is the standard deviation of population and n is number of observations.
is mean of sample, μ is the mean of population, σ is the standard deviation of population and n is number of observations.
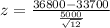
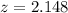
Hence, the value of the test statistic and degrees of freedom is 2.148 and 11 respectively.