Answer:
a)
6.33 x 10⁸ N/C
Direction : Towards negative charge.
b)
1.11125 x 10²⁰ m/s²
Direction : Towards positive charge.
Step-by-step explanation:
a)
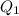 = magnitude of negative charge = 25 x 10⁻⁶ C
= magnitude of negative charge = 25 x 10⁻⁶ C
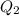 = magnitude of positive charge = 50 x 10⁻⁶ C
= magnitude of positive charge = 50 x 10⁻⁶ C
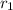 = distance of negative charge from point P = 0.02 m
= distance of negative charge from point P = 0.02 m
 = distance of positive charge from point P = 0.08 m
= distance of positive charge from point P = 0.08 m
Magnitude of electric field at P due to negative charge is given as
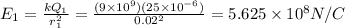
Magnitude of electric field at P due to positive charge is given as

Net electric field at P is given as
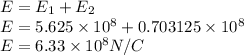
Direction:
Towards the negative charge.
b)
 = mass of the electron placed at P = 9.31 x 10⁻³¹ C
= mass of the electron placed at P = 9.31 x 10⁻³¹ C
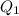 = magnitude of charge on electron = 1.6 x 10⁻¹⁹ C
= magnitude of charge on electron = 1.6 x 10⁻¹⁹ C
Acceleration of the electron due to the electric field at P is given as
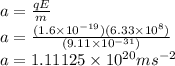
Direction: Towards the positive charge Since a negative charge experience electric force in opposite direction of the electric field.