Question

Write the equation in vertex form that has the root of -7 and has a vertex of (-1,-9)

Answer 1

`y=(1)/(4)(x+1)^2-9`

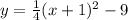
Explanation:

Method 1

we know that

The equation of a vertical parabola in vertex form is equal to

`y=a(x-h)^2+k`

where

a is the leading coefficient

(h,k) is the vertex

we have

(h,k)=(-1,-9)

substitute

`y=a(x+1)^2-9`

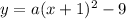
Remember that

one root is (-7,0)

substitute and solve for a

`0=a(-7+1)^2-9`

`0=a(-6)^2-9`

`0=36a-9`

`a=(1)/(4)`

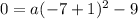
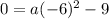
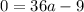
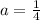
therefore

`y=(1)/(4)(x+1)^2-9`

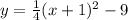
Method 2

I use the fact that the roots are the same distance from the vertex

the distance from the given root to the vertex is equal to

6 units

so

If one root is x=-7

then the other root is

x=-1+6=5

The general equation of the quadratic equation is equal to

`y=a(x+7)(x-5)`

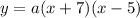
we have the vertex (-1,-9)

substitute the value of x and the value of y and solve for a

`-9=a(-1+7)(-1-5)`

`-9=a(6)(-6)`

`-9=-36a`

`a=(1)/(4)`

`y=(1)/(4)(x+7)(x-5)`

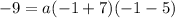
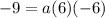
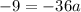
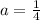
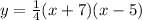
so

Expanded the equation, complete the square and rewrite as vertex form