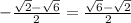Question

Use an Addition or Subtraction Formula to find the exact value of the expression, as demonstrated in Example 1. cos 41π 12.

Answer 1

Answer:
`(√(6)-√(2))/(2)`

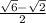
Explanation:

We apply the formula
`\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)`.

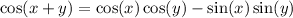Note that
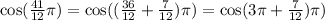`\cos((41)/(12)\pi)=\cos(((36)/(12)+(7)/(12))\pi)=\cos(3\pi + (7)/(12))\pi)`. Take
`x=3\pi` and
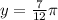`y=(7)/(12)\pi` in the formula above to get

`\cos((41)/(12)\pi)=\cos(3\pi)\cos((7)/(12)\pi)-\sin(3\pi)\sin((7)/(12)\pi)=(-1)\cdot \cos((7)/(12)\pi)-0\cdot\sin((7)/(12)\pi)=-\cos((7)/(12)\pi)`

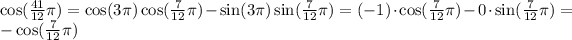
Then the value of this expression is
`-\cos((7)/(12)\pi)`

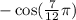
We can use the cosine addition formula again to simplify further. Decompose the fraction in the argument as:

`\cos((7)/(12)\pi)=\cos(((3)/(12)+(4)/(12))\pi)=\cos(((1)/(4)\pi + (1)/(3))\pi)`

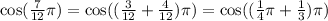
Applying the formula with
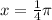`x=(1)/(4)\pi` and
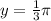`y=(1)/(3)\pi` we obtain

`\cos((7)/(12)\pi)=\cos((1)/(4)\pi)\cos((1)/(3)\pi)-\sin((1)/(4)\pi)\sin((1)/(3)\pi)=(√(2))/(2)\cdot(1)/(2) -(√(2))/(2)\cdot(√(3))/(2)=(√(2)-√(6))/(2)`

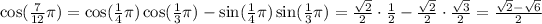
We conclude that this expression has the value
`-(√(2)-√(6))/(2)=(√(6)-√(2))/(2)`