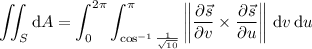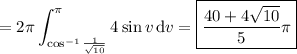Substituting
 from the cone's equation,
from the cone's equation,
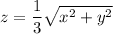
into the equation of the sphere,
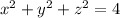
gives the intersection of the two surfaces,
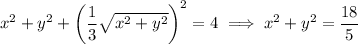
which is a circle of radius
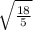 centered at
centered at
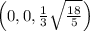 .
.
We parameterize this part of the sphere outside the cone (call it
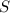 ) by
) by
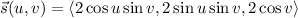
with
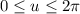 and
and
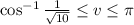 .
.
Take the normal vector to
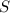 to be
to be
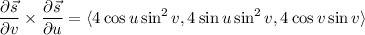
Then the area of
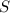 is
is