Question

If (3, 10) is the endpoint of a line segment, and

(-2, 3) is its midpoint, find the other endpoint.

Answer 1

The required points of the given line segment are ( - 7, - 4 ).

Explanation:

Given that the line segment AB whose midpoint M is ( - 2, 3 ) and point A is ( 3, 10), then we have to find point B of the line segment AB -

As we know that-

If a line segment AB is with endpoints (
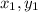`x_(1), y_(1)` ) and (
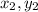`x_(2), y_(2)` )then the mid points M are-

M = (
`( x_(1) + x_(2) )/(2)` ,
`( y_(1) + y_(2) )/(2)` )

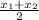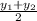Here,

Let A ( 3, 10 ), B ( x, y ) with midpoint M ( - 2, 3 ) -

then by the midpoint formula M are-

( - 2, 3 ) = (
`( 3 + x)/(2)` ,
`( 10 + y)/(2)` )

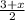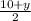On comparing x coordinate and y coordinate -

We get,

(
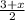`( 3 + x)/(2)` = - 2 ,
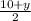`( 10 + y)/(2)` = 3)

( 3 + x = - 4, 10 + y = 6 )

( x = - 4 - 3, y = 6 - 10 )

( x = - 7, y = -4 )

Hence the required points A are ( - 7, - 4 ).

We can also verify by putting these points into Midpoint formula.