Question

Which graph represents the function f (x − 3), if f (x) = x2?

Answer 1

The answer is Y

Explanation:

Answer 2

Answer: See the graph attached.

Explanation:

Given the Quadratic function:

`f(x)=x^2`

We can identify that it is the "Parabola parent function". The parabola passes through the origin.

There are some tranformations for a function f(x). Two of them are the following:

If
`f(x+k)`, the function is shifted "k" units to the left.

If
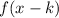`f(x-k)`, the function is shifted "k" units to the right.

Therefore, given that:

`f (x - 3)`

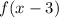
We can identify that this is the function
`f(x)=x^2` but shifted 3 units to the right:

`f (x - 3)=(x-3)^2`

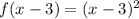
Knowing this, we can conclude that the graph that represents
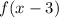`f (x - 3)` is the graph attached.