Question

Help please! (no one was answering it in physics and i really need help)

A cat is chasing a mouse across a 1.3 m tall dining table. The mouse darts to the side and the cat accidentally slides off, landing clumsily 0.75 m away from the edge of the table. How long did it take the cat to hit the ground?
0.78 seconds
0.51 seconds
0.27 seconds
0.95 seconds

Using the information you solved for in problem 9, how fast was the cat moving when it fell off the table?
2.97 m/s
1.45 m/s
3.81 m/s
6.93 m/s

Answer 1

Let
`v_0` be the cat's speed just as it leaves the edge of the table. Then taking the point 1.3 m below the edge of the table to be the origin, the cat's horizontal position at time
`t` is given by

`x(t)=v_0t`

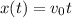
and its height is

`y(t)=1.3\,\mathrm m-gt^2`

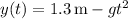
where
`g` is 9.8 m/s^2, the magnitude of the acceleration due to gravity.

The time it takes for the cat to hit the ground is
`t` with

`0=1.3\,\mathrm m-gt^2\implies t=\sqrt{\frac{1.3\,\rm m}g}\approx0.36\,\mathrm s`

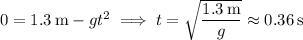
(Unfortunately, this doesn't match any of the given options...)

The cat lands 0.75 m away (horizontally) from the edge of the table, so that its speed
`v_0` was

`0.75\,\mathrm m=v_0(0.36\,\mathrm s)\implies v_0\approx2.08(\rm m)/(\rm s)`

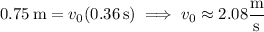
(Again, not one of the answer choices...)

I'm guessing there's either a typo in the question or answers.