Question

(a) Calculate the angular momentum of an ice skater spinning at 6.00 rev/s given his moment of inertia is 0.400kg·m2 . (b) He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his moment of inertia if his angular velocity decreases to 1.25 rev/s. (c) Suppose instead he keeps his arms in and allows friction of the ice to slow him to 3.00 rev/s. What average torque was exerted if this takes 15.0 s?

Answer 1

a) L = 15.08 kg*m^2/s

b) I = 1.92 kg*m^2

c) T = 0.5 N*m

Step-by-step explanation:

a) We know that:

L = IW

where L is the angular momentum, I the moment of inertia and W the angular velocity.

So, First, we change the angular velocity to rad/s

W = 6 rev/s = 37.7 rad/s

Then, replacing values on the equation, we get:

L = IW

L = (0.4)(37.7)

L = 15.08 kg*m^2/s

b) Using the conservation of the angular momentum:

`L_i = L_f`

`I_iW_i = I_fW_f`

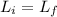
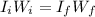
Where
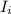`I_i` is the initial moment of inertia,
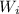`W_i` is the initial angular velocity,
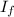`I_f` is the moment of inertia after he reduce his rate of spin and
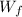`W_f` is the angular velocity after he reduce his rate of spin.

So, we change the final angular velocity to rad/s as:

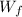`W_f` = 1.25 rev/s = 7.85 rad/s

Finally, replacing values and solving for I, we get:

(15.08 kg*m^2/s) = I(7.85rad/s)

I = 1.92 kg*m^2

c) We know that:

Τt =
`L_f -L_i`

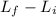
where T is the average torque, t the time,
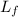`L_f` the final angular momentum and
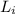`L_i` the initial angular momentum.

first we change the final angular velocity to rad/s:

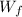`W_f` = 3 rev/s = 18.84 rad/s

so, replacing values, we get:

Τt =
`IW_f-IW_i`

Τ(15s) =
`(0.4)(18.84rad/s)-(0.4)(37.7rad/s)`

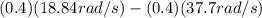
solving for T:

T = 0.5 N*m