Question

4. An object falls from the top of a storage cabinet 2 meters high. How

long does it take to reach the floor?

Answer 1

Time = 0.64 s

Step-by-step explanation:

Given:

Displacement of the storage cabinet is,
`S=2\ m`

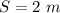
As the object falls from the top, so initial velocity is,
`u=0\ m/s`

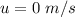
Also, the acceleration of the storage cabinet is due to gravity only.

So, acceleration of the storage cabinet is,
`a=9.8\ m/s^2`

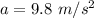
Now, in order to find the time taken to reach the floor, we have to use the equation of motion that relates displacement, initial velocity, acceleration and time.

So, the equation of motion used is given as:

`S=ut+(1)/(2)at^2`

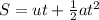
Plug in the given values and solve for time 't'. This gives,

`2=0+(1)/(2)(9.8)(t^2)\\\\2=4.9t^2\\\\t^2=(2)/(4.9)\\\\t^2=0.4082\\\\t=√(0.4082)\\\\t=0.64\ s`

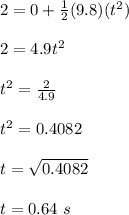
Therefore, the storage cabinet takes 0.64 seconds to reach the floor.