Question

How much ice would be needed if 150,000 J is absorbed in order to melt the ice?

Answer 1

449.1 g

Step-by-step explanation:

The second law of thermodynamics states that heat flows from hotter objects to colder ones. Assuming that
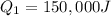`Q_1 = 150,000 J` is the heat given off by a substance in order to melt the ice, we also need to introduce the equation representing the melting of ice:

`Q_2 = \Delta H^o_(fus) m_(ice)`

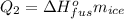
Since energy is conserved, the heat given off should be equal to the heat gained:

`Q_1 = Q_2`

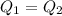
So that the equation becomes:

`\Delta H^o_(fus) m_(ice) = Q_1`

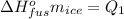
The enthalpy of fusion of ice is equal to:

`\Delta H^o_(fus) = 334 J/g`

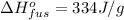
From here, rearrange the equation for the mass of ice:

`m_(ice) = (Q_1)/(\Delta H^o_(fus)) = (150,000 J)/(334 J/g) = 449.1 g`