Question

Use the given degree of confidence and sample data to construct a confidence interval for the population proportion p. A survey of 865 voters in one state reveals that 408 favor approval of an issue before the legislature. Construct the 95% confidence interval for the true proportion of all voters in the state who favor approval. A. 0.444 < p < 0.500 B. 0.438 < p < 0.505 C. 0.471 < p < 0.472 D. 0.435 < p < 0.508

Answer 1

Answer: Option 'c' is correct.

Explanation:

Since we have given that

Sample size = 865 = n

Number of voters favor approval of an issue before the legislature = 408 = x

So,
`\hat{p}=(x)/(n)=(408)/(865)=0.4716`

At 95% confidence level of significance, z = 1.96

So, confidence interval would be

`\hat{p}\pm z\sqrt{(p(1-p))/(n)}}\\=0.4716\pm 1.96* \sqrt{(0.4716* (1-0.4716))/(865)}}\\\\=0.4716\pm 0.00082222\\\\=(0.4716-0.00082222..,0.4716+0.00082222...)\\\\=(0.471,0.472)`

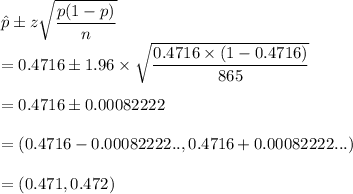
Hence, option 'c' is correct.