Question

On a coordinate plane, a dashed straight line has a negative slope and goes through (0, 2), and (1, negative 1). Everything to the right of the line is shaded. The solutions to the inequality y > −3x + 2 are shaded on the graph. Which point is a solution? (0, 2) (2, 0) (1, −2) (−2, 1)

Answer 1

(2,0)

Explanation:

Answer 2

(2,0)

Explanation:

we know that

If a ordered pair is a solution of the inequality, then the ordered pair must satisfy the inequality

we have

`y > -3x+2`

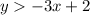
Substitute the value of x and the value of y of each point in the inequality and then compare the results

case a) (0, 2)

`2 > -3(0)+2`

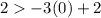
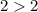`2 > 2` ----> is not true

so

the point not satisfy the inequality

therefore

The point is not a solution of the inequality

case b) (2,0)

`0 > -3(2)+2`

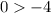`0 > -4` ----> is true

so

the point satisfy the inequality

therefore

The point is a solution of the inequality

case c) (1, -2)

`-2 > -3(1)+2`

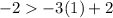
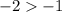`-2 > -1` ----> is not true

so

the point not satisfy the inequality

therefore

The point is not a solution of the inequality

case d) (-2, 1)

`1 > -3(-2)+2`

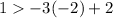
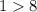`1 > 8` ----> is not true

so

the point not satisfy the inequality

therefore

The point is not a solution of the inequality

see the attached figure to better understand the problem