Question

An object is heated to 100°. It is left to cool in a room that

has a temperature of 30°. After 5 minutes, the temperature
of the object is 80°. What is the temperature of the object
after 20 minutes? When will the temperature of the object
be 35°?

Answer 1

Explanation:

Use Newton's Law of Cooling for this one. It involves natural logs and being able to solve equations that require natural logs. The formula is as follows:

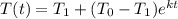`T(t)=T_(1)+(T_(0)-T_(1))e^(kt)` where

T(t) is the temp at time t

T₁ is the enviornmental temp

T₀ is the initial temp

k is the cooling constant which is different for everything, and

t is the time (here, it's in minutes)

If we are looking first for the temp after 20 minutes, we have to solve for the k value. That's what we will do first, given the info that we have:

T(t) = 80

T₁ = 30

T₀ = 100

t = 5

k = ?

Filling in to solve for k:

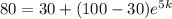`80=30+(100-30)e^(5k)` which simplifies to

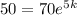`50=70e^(5k)` Divide both sides by 70 to get

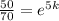`(50)/(70)=e^(5k)` and take the natural log of both sides:

`ln((5)/(7))=ln(e^(5k))`

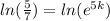
Since you're learning logs, I'm assuming that you know that a natural log and Euler's number, e, "undo" each other (just like taking the square root of something squared). That gives us:

`-.3364722366=5k`

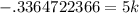
Divide both sides by 5 to get that

k = -.0672944473

Now that we have a value for k, we can sub that in to solve for T(20):

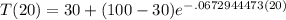`T(20)=30+(100-30)e^(-.0672944473(20))` which simplifies to

`T(20)=30+70e^(-1.345888946)`

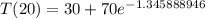
On your calculator, raise e to that power and multiply that number by 70:

T(20)= 30 + 70(.260308205) and

T(20) = 30 + 18.22157435 so

T(20) = 48.2°

Now we can use that k value to find out when (time) the temp of the object cools to 35°:

T(t) = 35

T₁ = 30

T₀ = 100

k = -.0672944473

t = ?

`35=30+100-30)e^(-.0672944473t)` which simplifies to

`5=70e^(-.0672944473t)`

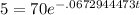
Now divide both sides by 70 and take the natural log of both sides:

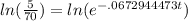`ln((5)/(70))=ln(e^(-.0672944473t))` which simplifies to

-2.63905733 = -.0672944473t

Divide to get

t = 39.2 minutes