Question

The U.S. Department of Agriculture claims that the mean consumption of bottled water by a person in the United States is 28.5 gallons per year. You believe that a person consume more than 28.5 gallons in bottled water per year. A random sample of 100 people in the United States has a mean bottled water consumption of 27.8 gallons per year with a standard deviation of 4.1 gallons. At α = 0.10 significance level can you reject the claim?

Answer 1

Answer: No

Explanation:

Let
`\mu` be the population mean .

As per given , we have to test the hypothesis.

`H_0:\mu=28.5\\\\ H_a:\mu>28.5`

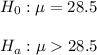
∵ Alternative hypothesis (
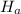`H_a`) is right-tailed , so our test is a right-tailed test.

Also, the population standard deviation is unknown to be 0.8 , so we use t-test.

Test statistic:
`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

, where
`\overline{x}` = Sample mean

`\mu` = population mean

`s` = sample standard deviation.

n= Sample size

Substitute
`\overline{x}=27.8`

`s=4.1`

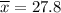
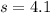
n= 100 , we get

`t=(27.8-28.5)/((4.1)/(√(100)))`

`t=(-0.7)/((4.1)/(√(10)))\approx-1.71`

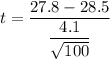
By t-distribution, the critical t-value for degree of freedom 99 ( df =n-1) and significance level 0.10 :

`t_(\alpha,df)=1.29`

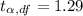
Decision : ∵ Calculated -value (-1.71) < Critical value (1.29).

It means we do not reject the null hypothesis.

Conclusion : We do not have sufficient evidence at α = 0.10 significance level to reject the claim that the mean consumption of bottled water by a person in the United States is 28.5 gallons per year