Answer:
t = 1.07 seg
Step-by-step explanation:
First we are going to solve the differential equation for the velocity:
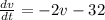
This is a differential equation of separable variables
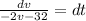
Multiplying by -1 to both sides of the equation
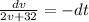
We integrate the left side with respect to the velocity and the right side with respect to time

where k is a integration constant
ln(2v+32) = -2t + k
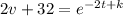
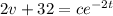
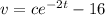
We determine the constant c with the initial condition v(0) = -50
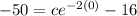
-50 + 16 = c
c = -34
Then
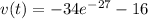
When the velocity is -20 ft/s the time is:
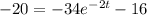
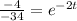
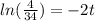
t = 1.07 seg