Answer:
The inequality is
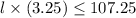
Explanation:
Given: Area of volleyball net=
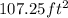
Width of Volleyball net=
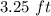
Considering the volleyball net is in rectangular shape and l and w is length and width respectively.
Area of rectangle=
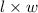
Now, using formula to form inequality
⇒
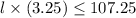
Next, using the inequality to find length of Volleyball net.
∴
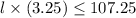
Dividing both side by 3.25
⇒
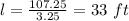
∴ l= 33 ft
The possible length of Volleyball net is 33 ft.