Question

The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. The probability that there are 8 occurrences in ten minutes is

A. .0241
B. .0771
C. .1126
D. .9107

Answer 1

The probability that there are 8 occurrences in ten minutes is

option B. 0 .0771

Explanation:

Given:

Random Variable = x

Mean number of occurrences in ten minutes is 5.3.

The probability of an occurrence is the same in any two time periods of an equal length

To Find:

The probability that there are 8 occurrences in ten minutes = ?

Solution:

Let X be the number of occurrences of the event X

`X \sim {Pois} (\lambda)`

`\lambda = E(X) = 5.3`

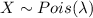
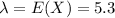
Possion of distribution is given by ,

`P(X=x) = (e^(- \lambda) \lambda^(x))/(x!)`

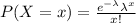
Substituting the values,

`P(X=8) = (e^(- 5.3) 5.3^(8))/(8!)`

`P(X=8) = ((0.004994) ( 622596.904))/(40320)`

`P(X=8) = ((3109.24894))/(40320)`

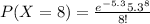
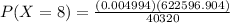
P(X=8) = 0.0771