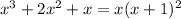Factor x3 + 2x2 + x completely. (x + 1)2 x(x2 + 1) x(x + 1)2

Question

asked Jul 20, 2020 216k views

2 Answers

FredericK · Answer 1 · 2020-07-26T14:21:06+0000

Answer:

Explanation:

Given:

The expression to factor is given as:

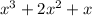
x^3+2x^2+x

In order to factor it, we write the factors of each of the terms of the given polynomial. So,

The factors of the three terms are:

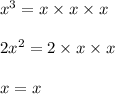
$x^3=x* x* x\\\\2x^2=2* x* x\\\\x=x$

Now, 'x' is a common factor for all the three terms. So, we factor it out. This gives,

$x((x^3)/(x)+2(x^2)/(x)+(x)/(x))\\\\x(x^2+2x+1)$

Now, we know a identity which is given as:

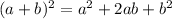
(a+b)^2=a^2+2ab+b^2

Here,
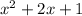x^2+2x+1 can be rewritten as
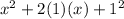
x^2+2(1)(x)+1^2

So,
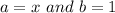
$a=x\ and\ b=1$

Thus,
x^2+2(1)(x)+1^2= (x+1)^2

Therefore, the complete factorization of the given expression is:

x^3+2x^2+x=x(x+1)^2