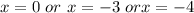Answer:
Therefore the THREE roots are
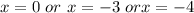
Explanation:
Given:
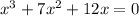
To Find:
All the Roots = ?
Solution:
As the degree of the polynomial is THREE then the number of root are also THREE.

Now one root is Zero For other we need to Factorize
So by Splitting the middle term
i.e Factor of 12 such that sum should be 7
i.e 3 × 4 = 12 and 3 + 4 = 7
∴

Therefore the THREE roots are