The function
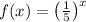 is decaying.
is decaying.
Explanation:
Given:
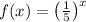
The above equation can also write as below,
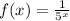
Now from the function we can see that as we are increasing the value of x the value of function is decreasing. Let take some values of x and then find out the value of function at those value of x
When x = 1 ,
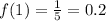
When x = 2,

When x = 3,
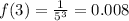
So, from the above examples, we can see that the value of function is decreasing on increasing the value of x. Hence the function is decay