Question

Nielsen Media Research wants to estimate the mean amount of time, in minutes, that full-time college students spend texting each weekday.Find the sample size necessary to estimate that mean with a 15 minute margin of error. Assume that a 96% confidence level is desired and that the standard deviation is estimated to be 112.2 minutes.

Answer 1

n=237

Explanation:

Previous concepts

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Assuming the X follows a normal distribution

`X \sim N(\mu, \sigma=112.2)`

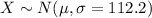
We know that the margin of error for a confidence interval is given by:

`Me=z_(\alpha/2)(\sigma)/(√(n))` (1)

The next step would be find the value of
`\z_(\alpha/2)`,
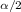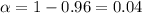`\alpha=1-0.96=0.04` and
`\alpha/2=0.02`

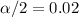
Using the normal standard table, excel or a calculator we see that:

`z_(\alpha/2)=2.054`

If we solve for n from formula (1) we got:

`√(n)=(z_(\alpha/2) \sigma)/(Me)`

`n=((z_(\alpha/2) \sigma)/(Me))^2`

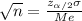
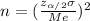
And we have everything to replace into the formula:

`n=((2.054(112.2))/(15))^2 =236.05`

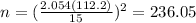
And if we round up the answer we see that the value of n to ensure the margin of error required
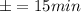`\pm=15 min` is n=237.