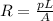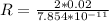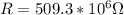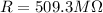For the calculation of resistance there are generally two paths. The first is through Ohm's law and the second is through the relationship
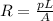
Where
p = Specific resistance of material
L = Length
A = Area
The area of nerve axon is given as
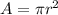
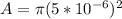
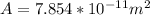
The rest of values are given as
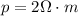

Therefore the resistance is