Question

Air enters a turbine operating at steady state at 8 bar, 1400 K and expands to 0.8 bar. The turbine is well insulated, and kinetic and potential energy effects can be neglected. Assuming ideal gas behavior for the air, what is the maximum theoretical work that could be developed by the turbine in kJ per kg of air flow?

Answer 1

To solve this problem it is necessary to apply the concepts related to the adiabatic process that relate the temperature and pressure variables

Mathematically this can be determined as

`(T_2)/(T_1) = ((P_2)/(P_1))^{((\gamma-1)/(\gamma))}`

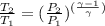
Where

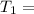`T_1 =`Temperature at inlet of turbine

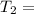`T_2 =` Temperature at exit of turbine

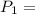`P_1 =` Pressure at exit of turbine

`P_2 =`Pressure at exit of turbine

The steady flow Energy equation for an open system is given as follows:

`m_i = m_0 = m`

`m(h_i+(V_i^2)/(2)+gZ_i)+Q = m(h_0+(V_0^2)/(2)+gZ_0)+W`

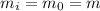
Where,

m = mass

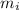`m_i` = mass at inlet

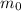`m_0`= Mass at outlet

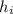`h_i` = Enthalpy at inlet

`h_0` = Enthalpy at outlet

W = Work done

Q = Heat transferred

`V_i` = Velocity at inlet

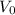`V_0`= Velocity at outlet

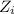`Z_i`= Height at inlet

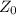`Z_0`= Height at outlet

For the insulated system with neglecting kinetic and potential energy effects

`h_i = h_0 + W`

`W = h_i -h_0`

Using the relation T-P we can find the final temperature:

`(T_2)/(T_1) = ((P_2)/(P_1))^{((\gamma-1)/(\gamma))}`

`(T_2)/(1400K) = ((0.8bar)/(8nar))^{((1.4-1)/(1.4))}`

`T_2 = 725.126K`

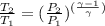
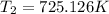
From this point we can find the work done using the value of the specific heat of the air that is 1,005kJ / kgK

So:

`W = h_i -h_0`

`W = C_p (T_1-T_2)`

`W = 1.005(1400-725.126)`

`W = 678.248kJ/Kg`

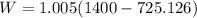
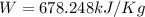
Therefore the maximum theoretical work that could be developed by the turbine is 678.248kJ/kg