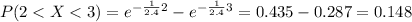Question

slader The magnitude of earthquakes recorded in a region of North America can be modeled ashaving an exponential distribution with mean 2.4, as measured on the Richter scale. Find theprobability that an earthquake striking this region will a exceed 3.0 on the Richter scale. b fall between 2.0 and 3.0 on the Richter scale.

Answer 1

a)
`P(X>3.0)=1-P(X \leq 3.0)= 1- [1- e^{-(1)/(2.4) 3.0}]=e^{-(1)/(2.4) 3.0}=0.287`

b)
`P(2<X<3)= 1- e^{-(1)/(2.4) 3} -[ 1- e^{-(1)/(2.4) 2}]`

`P(2<X<3)=e^{-(1)/(2.4) 2}- e^{-(1)/(2.4) 3}=0.435-0.287=0.148`

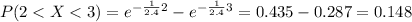
Explanation:

Definitions and concepts

The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:

`P(X=x) =\lambda^x (e^(-\lambda))/(x!)`

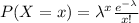
And the parameter
`\lambda` represent the average ocurrence rate per unit of time.

The exponential distribution is useful when we want to describ the waiting time between Poisson occurrences. If we assume that the random variable T represent the waiting time btween two consecutive event, we can define the probability that 0 events occurs between the start and a time t, like this:

`P(X>x)= e^(-\lambda x)`

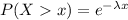
We can express in terms of the mean
`\mu =(1)/(\lambda)`

`P(X>x)= e^{-(1)/(\mu) x}`

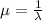
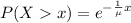
And the cumulative function would be given by the complement rule like this:

`P(X\leq x)=1- e^{-(1)/(\mu) x}`

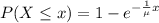
Solution for the problem

For this case we have that X the random variable that represent the magnitude of earthquakes recorded in a region of North America, we know that the distribution is given by:

`X\sim Expon(\mu =2.4)`

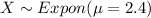
a) Find theprobability that an earthquake striking this region will a exceed 3.0 on the Richter scale

So for this case we want this probability:

`P(X>3.0)=1-P(X \leq 3.0)= 1- [1- e^{-(1)/(2.4) 3.0}]=e^{-(1)/(2.4) 3.0}=0.287`

b) fall between 2.0 and 3.0 on the Richter scale.

For this case we want this probability:

`P(2 < X <3) = P(X<3) -P(X<2)`

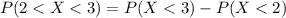
And replacing we have this:

`P(2<X<3)= 1- e^{-(1)/(2.4) 3} -[ 1- e^{-(1)/(2.4) 2}]`

`P(2<X<3)=e^{-(1)/(2.4) 2}- e^{-(1)/(2.4) 3}=0.435-0.287=0.148`