Question

Starting from rest at a height equal to the radius of the circular track, a block of mass 24 kg slides down a quarter circular track under the influence of gravity with friction present (of coefficient µ). The radius of the track is 15 m. The acceleration of gravity is 9.8 m/s 2 .Starting from rest at a height equal to the radius of the circular track, a block of mass 24 kg slides down a quarter circular track under the influence of gravity with friction present (of coefficient µ). The radius of the track is 15 m. The acceleration of gravity is 9.8 m/s 2 . If the kinetic energy of the block at the

bottom of the track is 3900 J, what is the

work done against friction?

Answer in units of J.

Answer 1

The work done against friction is 372 joules

Step-by-step explanation:

It is given that,

Mass of block, m = 24 kg

Radius of the track, r = 15 m

Acceleration due to gravity,
`a=9.8\ m/s^2`

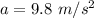
If the kinetic energy of the block at the bottom of the track is, 3900 J

Let P is the work done against friction. It is given by :

`P=mgh`

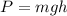
Here, h = r

`P=24\ kg* 9.8\ m/s^2* 15\ m`

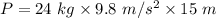
P = 3528 J

Since it ends up with 3900 J, the work done is given by or the lost in energy will be :

W = 3900 - 3528

W = 372 joules

So, the work done against friction is 372 joules. Hence, this is the required solution.