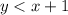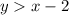Answer:
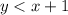
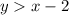
Explanation:
According to the graph, the system is formed by two inequalities. Let's find out the equation to each line in first place.
Notice that the upper line passes through points (-1,0) and (0,1). First, we find its slope

Then, we use the point-slope formula to find the equation
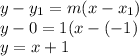
Now, the dashed line indiactes that the inequalities must have sings < or >.
Notice that point (0,0) is part of its solution, that means the inequality is
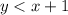
We do the same process to find the other inequality.
The line passes through points (0,-2) and (2,0).
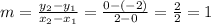
Then,
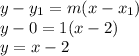
Notice that point (0,0) is part of its solution, so the inequality is
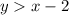
Therefore, the system of inequalities is