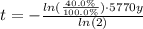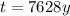Answer:
7628 y
Step-by-step explanation:
Carbon-14 is radioactive and it follows the first-order kinetics for a radioactive decay. The first-order kinetics may be described by the following integrated rate law:
![ln(([A]_t)/([A]_o))=-kt](https://img.qammunity.org/2020/formulas/chemistry/middle-school/orvg4loiq6j8ax9tumz23mfkor1zio6prn.png)
Here:
![[A]_t](https://img.qammunity.org/2020/formulas/chemistry/middle-school/qwbo51w0b2s8i03byawrdg0o7vt4t47aqo.png) is the mass, moles, molarity or percentage of the material left at some time of interest t;
is the mass, moles, molarity or percentage of the material left at some time of interest t;
![[A]_o](https://img.qammunity.org/2020/formulas/chemistry/college/vfm07rqugmdqisio26k7clnl28e24vlfox.png) is the mass, moles, molarity or percentage of the material initially, we know that initially we expect to have 100 % of carbon-14 before it starts to decay;
is the mass, moles, molarity or percentage of the material initially, we know that initially we expect to have 100 % of carbon-14 before it starts to decay;
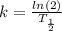 is the rate constant;
is the rate constant;
 is time.
is time.
The equation becomes:
![ln(([A]_t)/([A]_o))=-\frac{ln(2)}{T_{(1)/(2)}}t](https://img.qammunity.org/2020/formulas/chemistry/middle-school/x01paq44n94hzz6pkpfktsi0mgf9qfubo6.png)
Given:
![([A]_t)/([A]_o) = (40.0 %)/(100.0 %)]()
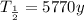
Solve for time:
![t = -\frac{ln(([A]_t)/([A]_o))\cdot T_{(1)/(2)}}{ln(2)}](https://img.qammunity.org/2020/formulas/chemistry/middle-school/ru795ymr0pnukbmrf8mofbp3dsiaty4321.png)
In this case: