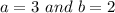Question

Rewrite x2 − 6x + 7 = 0 in the form (x − a)2 = b, where a and b are integers, to determine the a and b values.

Answer 1: a = 4 and b = 3
Answer 2: a = 3 and b = 2
Answer 3: a = 2 and b = 1
Anwser 4: a = 1 and b = 4

Answer 1

Answer 2: a = 3 and b = 2

Answer 2

Therefore values of a and b are

`a=3\ and\ b = 2`

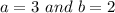
Explanation:

Rewrite
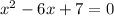`x^(2)-6x+7=0` in the form

`(x-a)^(2)=b`

where a and b are integers,

To Find:

a = ?

b = ?

Solution:

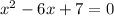`x^(2)-6x+7=0` ..............Given

Which can be written as

`x^(2)-6x=-7`

`((1)/(2) coefficient\ of\ x)^(2)=((1)/(2)* -6)^(2)=9`

Adding half coefficient of X square on both the side we get

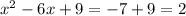`x^(2)-6x+9=-7+9=2` ...................( 1 )

By identity we have (A - B)² =A² - 2AB + B²

Therefore,

`x^(2)-6x+9=x^(2)-2* 3* x+3^(2)=(x-3)^(2)`

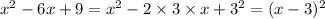
Substituting in equation 1 we get

`(x-3)^(2)=2`

Which is in the form of

`(x-a)^(2)=b`

On comparing we get

a = 3 and b = 2

Therefore values of a and b are

`a=3\ and\ b = 2`