Answer:
The number of years in which saving gets double is 8 years .
Explanation:
Given as :
The principal amount saved into the account = p = $8,000
The rate of interest applied = r = 9%
The Amount gets double in n years = $A
Or, $A = 2 × p = $8,000 × 2 = $16,000
Let the number of years in which saving gets double = n years
Now, From Compound Interest method
Amount = Principal ×
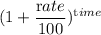
Or, 2 × p = p ×
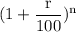
Or, $16,000 = $8,000 ×
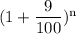
Or,
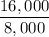 =
=
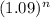
Or, 2 =
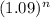
Now, Taking Log both side
 2 =
2 =

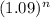
Or, 0.3010 = n ×
 1.09
1.09
Or, 0.3010 = n × 0.0374
∴ n =
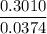
I.e n = 8.04 ≈ 8
So, The number of years = n = 8
Hence, The number of years in which saving gets double is 8 years . Answer