Answer:
AB = √116 ≈ 10.77
Explanation:
Use the formula that calculate the distance between two points:
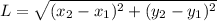
L means length
For the x and y, substitute a coordinate value that you will label as set 1 or 2.
For example:
A (-3, 7) will be set 1. x₁ = -3 y₁ = 7
B (7 , 3) will be set 2. x₂ = 7 y₂ = 3
Substitute the points into the formula to find the length AB. Simplify.
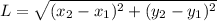
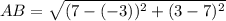 Solve inside the brackets first
Solve inside the brackets first
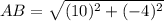 Square each term under the root
Square each term under the root
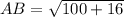 Add under the root
Add under the root
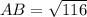 Final exact answer is radical (root) form
Final exact answer is radical (root) form
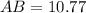 Final approximate or rounded answer to 2 decimals
Final approximate or rounded answer to 2 decimals
The length of AB is the squareroot of 116, or about 10.77 units.