Question

12-sqrt(-8)
Complex number notation

Answer 1

The complex number notation of 12-sqrt(-8) is 12 - 2.828i

Explanation:

Given:

12-sqrt(-8)

To Find:

The complex number notation of 12-sqrt(-8)

Solution:

12-sqrt(-8) can be
`12-√((8)`

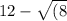
where
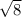`√(8)` can be written as

`\sqrt {4 \cdot 2 \cdot -1}`

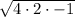
Now using the below radical rule which states that

`√(a \cdot b) = √(a) \cdot √(b)`

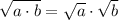
Then,

`\sqrt {4 \cdot 2 \cdot (-1)}`

=>
`\sqrt {4} \cdot \sqrt {2} \cdot \sqrt { -1}`

=>
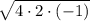
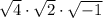
`2 \cdot \sqrt {2} \cdot \sqrt {-1}`-----------------(1)

Also we know that

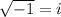`\sqrt {-1}= i`---------------------(2)

substituting (2) in (1)

we get

=>
`2 \cdot \sqrt {2} \cdot i`

=>
`2i \cdot \sqrt {2}`

=>
`2i \cdot 1.414`

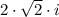
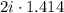
=> 2.828i