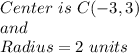Answer:
Therefore,
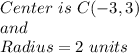
Explanation:
Given:
A Equation of a Circle that is
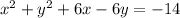
Which can be written as
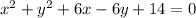
To Find:
Center C( -g , -f ) = ?
radius = r =?
Solution:
General Equation of a Circle is given as
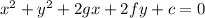
On Comparing the Given equation with the General equation we get the following values,
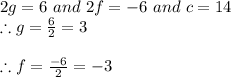
Now, Center and Radius for above circle is given as

Therefore,